E6C : 6-circle diffractometer example#

The 6-circle diffractometer can be considered as a 4-circle diffractometer with two additional rotations that rotate the sample and detector separately about the $\vec z$ axis.

$Schematic of a 6-circle diffractometer$

Note: This example is available as a Jupyter notebook from the hklpy source code website: bluesky/hklpy

Setup the E6C diffractometer in hklpy#

In hkl E6C geometry (https://people.debian.org/~picca/hkl/hkl.html#orge5e0490):

xrays incident on the $\vec{x}$ direction (1, 0, 0)

axis	moves	rotation axis	vector
mu	sample	$\vec{z}$	`[0 0 1]`
omega	sample	$-\vec{y}$	`[0 -1 0]`
chi	sample	$\vec{x}$	`[1 0 0]`
phi	sample	$-\vec{y}$	`[0 -1 0]`
gamma	detector	$\vec{z}$	`[0 0 1]`
delta	detector	$-\vec{y}$	`[0 -1 0]`

Define this diffractometer#

Create a Python class that specifies the names of the real-space positioners. We call it SixCircle here but that choice is arbitrary. Pick any valid Python name not already in use. The convention is to start Python class names with a capital letter and use CamelCase to mark word starts.

The argument to the SixCircle class tells which hklpy base class will be used. This sets the geometry. (The class we show here could be replaced entirely with hkl.geometries.SimulatedE6C but we choose to show here the complete steps to produce that class.) The hklpy documentation provides a complete list of diffractometer geometries.

In hklpy, the reciprocal-space axes are known as pseudo positioners while the real-space axes are known as real positioners. For the real positioners, it is possible to use different names than the canonical names used internally by the hkl library. That is not covered here.

Note: The keyword argument kind="hinted" is an indication that this signal may be plotted.

This SixCircle() class example uses simulated motors. See the drop-down for an example how to use EPICS motors.

SixCircle() class using EPICS motors

from hkl import E6C
from ophyd import EpicsMotor, PseudoSingle
from ophyd import Component as Cpt

class SixCircle(E6C):
    """
    Our 6-circle.  Eulerian.
    """
    # the reciprocal axes are called "pseudo" in hklpy
    h = Cpt(PseudoSingle, '', kind="hinted")
    k = Cpt(PseudoSingle, '', kind="hinted")
    l = Cpt(PseudoSingle, '', kind="hinted")

    # the motor axes are called "real" in hklpy
    mu = Cpt(EpicsMotor, "pv_prefix:m42", kind="hinted")
    omega = Cpt(EpicsMotor, "pv_prefix:m41", kind="hinted")
    chi = Cpt(EpicsMotor, "pv_prefix:m22", kind="hinted")
    phi = Cpt(EpicsMotor, "pv_prefix:m35", kind="hinted")
    gamma = Cpt(EpicsMotor, "pv_prefix:m7", kind="hinted")
    delta = Cpt(EpicsMotor, "pv_prefix:m8", kind="hinted")

[1]:

from hkl import E6C, SimMixin
from ophyd import SoftPositioner
from ophyd import Component as Cpt

class SixCircle(SimMixin, E6C):
    """
    Our 6-circle.  Eulerian.
    """
    # the reciprocal axes are defined by SimMixin

    mu = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)
    omega = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)
    chi = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)
    phi = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)
    gamma = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)
    delta = Cpt(SoftPositioner, kind="hinted", limits=(-180, 180), init_pos=0)

Create the Python diffractometer object (sixc) using the SixCircle() class. By convention, the name keyword is the same as the object name.

[2]:

sixc = SixCircle("", name="sixc")

Add a sample with a crystal structure#

[3]:

from hkl import Lattice
from hkl import SI_LATTICE_PARAMETER

# add the sample to the calculation engine
a0 = SI_LATTICE_PARAMETER
sixc.calc.new_sample(
    "silicon",
    lattice=Lattice(a=a0, b=a0, c=a0, alpha=90, beta=90, gamma=90)
    )

[3]:

HklSample(name='silicon', lattice=LatticeTuple(a=5.431020511, b=5.431020511, c=5.431020511, alpha=90.0, beta=90.0, gamma=90.0), ux=Parameter(name='None (internally: ux)', limits=(min=-180.0, max=180.0), value=0.0, fit=True, inverted=False, units='Degree'), uy=Parameter(name='None (internally: uy)', limits=(min=-180.0, max=180.0), value=0.0, fit=True, inverted=False, units='Degree'), uz=Parameter(name='None (internally: uz)', limits=(min=-180.0, max=180.0), value=0.0, fit=True, inverted=False, units='Degree'), U=array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]]), UB=array([[ 1.15690694e+00, -7.08401189e-17, -7.08401189e-17],
       [ 0.00000000e+00,  1.15690694e+00, -7.08401189e-17],
       [ 0.00000000e+00,  0.00000000e+00,  1.15690694e+00]]), reflections=[])

Setup the UB orientation matrix using hklpy#

Define the crystal’s orientation on the diffractometer using the 2-reflection method described by Busing & Levy, Acta Cryst 22 (1967) 457.

Set the same X-ray wavelength for both reflections, by setting the diffractometer energy#

[4]:

from hkl import A_KEV
sixc.energy.put(A_KEV / 1.54)  # (8.0509 keV)

Find the first reflection and identify its Miller indices: (hkl)#

[5]:

r1 = sixc.calc.sample.add_reflection(
    4, 0, 0,
    position=sixc.calc.Position(
        delta=69.0966,
        omega=-145.451,
        chi=0,
        phi=0,
        mu=0,
        gamma=0,
    )
)

Find the second reflection#

[6]:

r2 = sixc.calc.sample.add_reflection(
    0, 4, 0,
    position=sixc.calc.Position(
        delta=69.0966,
        omega=-145.451,
        chi=90,
        phi=0,
        mu=0,
        gamma=0,
    )
)

Compute the UB orientation matrix#

The add_reflection() method uses the current wavelength at the time it is called. (To add reflections at different wavelengths, change the wavelength before calling add_reflection() each time.) The compute_UB() method returns the computed UB matrix. Ignore it here.

[7]:

sixc.calc.sample.compute_UB(r1, r2)

[7]:

array([[-1.41342846e-05, -1.41342846e-05, -1.15690694e+00],
       [ 0.00000000e+00, -1.15690694e+00,  1.41342846e-05],
       [-1.15690694e+00,  1.72682934e-10,  1.41342846e-05]])

Report what we have setup#

[8]:

sixc.pa()

===================== ========================================================================================================
term                  value
===================== ========================================================================================================
diffractometer        sixc
geometry              E6C
class                 SixCircle
energy (keV)          8.05092
wavelength (angstrom) 1.54000
calc engine           hkl
mode                  bissector_vertical
positions             ===== =======
                      name  value
                      ===== =======
                      mu    0.00000
                      omega 0.00000
                      chi   0.00000
                      phi   0.00000
                      gamma 0.00000
                      delta 0.00000
                      ===== =======
constraints           ===== ========= ========== ===== ====
                      axis  low_limit high_limit value fit
                      ===== ========= ========== ===== ====
                      mu    -180.0    180.0      0.0   True
                      omega -180.0    180.0      0.0   True
                      chi   -180.0    180.0      0.0   True
                      phi   -180.0    180.0      0.0   True
                      gamma -180.0    180.0      0.0   True
                      delta -180.0    180.0      0.0   True
                      ===== ========= ========== ===== ====
sample: silicon       ================= ======================================================================================
                      term              value
                      ================= ======================================================================================
                      unit cell edges   a=5.431020511, b=5.431020511, c=5.431020511
                      unit cell angles  alpha=90.0, beta=90.0, gamma=90.0
                      ref 1 (hkl)       h=4.0, k=0.0, l=0.0
                      ref 1 positioners mu=0.00000, omega=-145.45100, chi=0.00000, phi=0.00000, gamma=0.00000, delta=69.09660
                      ref 2 (hkl)       h=0.0, k=4.0, l=0.0
                      ref 2 positioners mu=0.00000, omega=-145.45100, chi=90.00000, phi=0.00000, gamma=0.00000, delta=69.09660
                      [U]               [[-1.22173048e-05 -1.22173048e-05 -1.00000000e+00]
                                         [ 0.00000000e+00 -1.00000000e+00  1.22173048e-05]
                                         [-1.00000000e+00  1.49262536e-10  1.22173048e-05]]
                      [UB]              [[-1.41342846e-05 -1.41342846e-05 -1.15690694e+00]
                                         [ 0.00000000e+00 -1.15690694e+00  1.41342846e-05]
                                         [-1.15690694e+00  1.72682934e-10  1.41342846e-05]]
                      ================= ======================================================================================
===================== ========================================================================================================

[8]:

<pyRestTable.rest_table.Table at 0x7f7a36909b50>

Check the orientation matrix#

Perform checks with forward (hkl to angle) and inverse (angle to hkl) computations to verify the diffractometer will move to the same positions where the reflections were identified.

Constrain the motors to limited ranges#

allow for slight roundoff errors
keep delta in the positive range
keep omega in the negative range
keep gamma, mu, & phi fixed at zero

First, we apply constraints directly to the calc-level support.

[9]:

sixc.calc["delta"].limits = (-0.001, 180)
sixc.calc["omega"].limits = (-180, 0.001)

for nm in "gamma mu phi".split():
    getattr(sixc, nm).move(0)
    sixc.calc[nm].value = 0
    sixc.calc[nm].limits = (0, 0)
sixc.engine.mode = "constant_phi_vertical"
sixc.show_constraints()

===== ========= ========== ===== ====
axis  low_limit high_limit value fit
===== ========= ========== ===== ====
mu    0.0       0.0        0.0   True
omega -180.0    0.001      0.0   True
chi   -180.0    180.0      0.0   True
phi   0.0       0.0        0.0   True
gamma 0.0       0.0        0.0   True
delta -0.001    180.0      0.0   True
===== ========= ========== ===== ====

[9]:

<pyRestTable.rest_table.Table at 0x7f7a34681dd0>

Next, we show how to use additional methods of Diffractometer() that support undo and reset features for applied constraints. The support is based on a stack (a Python list). A set of constraints is added (apply_constraints()) or removed (undo_last_constraints()) from the stack. Or, the stack can be cleared (reset_constraints()).

method	what happens
`apply_constraints()`	Add a set of constraints and use them
`undo_last_constraints()`	Remove the most-recent set of constraints and restore the previous one from the stack.
`reset_constraints()`	Set constraints back to initial settings.
`show_constraints()`	Print the current constraints in a table.

A set of constraints is a Python dictionary that uses the real positioner names (the motors) as the keys. Only those constraints with changes need be added to the dictionary but it is permissable to describe all the real positioners. Each value in the dictionary is a hkl.diffract.Constraint, where the values are specified in this order: low_limit, high_limit, value, fit.

Apply new constraints using the applyConstraints() method. These add to the existing constraints, as shown in the table.

[10]:

from hkl import Constraint
sixc.apply_constraints(
    {
        "delta": Constraint(-0.001, 90, 0, True),
        "chi": Constraint(-90, 90, 0, True),
    }
)
sixc.show_constraints()

===== ========= ========== ===== ====
axis  low_limit high_limit value fit
===== ========= ========== ===== ====
mu    0.0       0.0        0.0   True
omega -180.0    0.001      0.0   True
chi   -90.0     90.0       0.0   True
phi   0.0       0.0        0.0   True
gamma 0.0       0.0        0.0   True
delta -0.001    90.0       0.0   True
===== ========= ========== ===== ====

[10]:

<pyRestTable.rest_table.Table at 0x7f7a346616d0>

Then remove (undo) those new additions.

[11]:

sixc.undo_last_constraints()
sixc.show_constraints()

===== ========= ========== ===== ====
axis  low_limit high_limit value fit
===== ========= ========== ===== ====
mu    0.0       0.0        0.0   True
omega -180.0    0.001      0.0   True
chi   -180.0    180.0      0.0   True
phi   0.0       0.0        0.0   True
gamma 0.0       0.0        0.0   True
delta -0.001    180.0      0.0   True
===== ========= ========== ===== ====

[11]:

<pyRestTable.rest_table.Table at 0x7f7a3467c2d0>

(400) reflection test#

Check the inverse (angles -> (hkl)) computation.
Check the forward ((hkl) -> angles) computation.

Check the inverse calculation: (400)#

To calculate the (hkl) corresponding to a given set of motor angles, call fourc.inverse((h, k, l)). Note the second set of parentheses needed by this function.

The values are specified, without names, in the order specified by fourc.calc.physical_axis_names.

[12]:

print("axis names:", sixc.calc.physical_axis_names)

axis names: ['mu', 'omega', 'chi', 'phi', 'gamma', 'delta']

Now, proceed with the inverse calculation.

[13]:

sol = sixc.inverse((0, -145.451, 0, 0, 0, 69.0966))
print(f"(4 0 0) ? {sol.h:.2f} {sol.k:.2f} {sol.l:.2f}")

(4 0 0) ? 4.00 0.00 0.00

Check the forward calculation: (400)#

Compute the angles necessary to position the diffractometer for the given reflection.

Note that for the forward computation, more than one set of angles may be used to reach the same crystal reflection. This test will report the default selection. The default selection (which may be changed through methods described in the hkl.calc module) is the first solution.

function	returns
`sixc.forward()`	The default solution
`sixc.calc.forward()`	List of all allowed solutions.

[14]:

sol = sixc.forward((4, 0, 0))
print(
    "(400) :",
    f"tth={sol.delta:.4f}",
    f"omega={sol.omega:.4f}",
    f"chi={sol.chi:.4f}",
    f"phi={sol.phi:.4f}",
    f"mu={sol.mu:.4f}",
    f"gamma={sol.gamma:.4f}",
    )

(400) : tth=69.0982 omega=-145.4502 chi=-0.0000 phi=0.0000 mu=0.0000 gamma=0.0000

(040) reflection test#

Repeat the inverse and forward calculations for the second orientation reflection.

Check the inverse calculation: (040)#

[15]:

sol = sixc.inverse((0, -145.451, 90, 0, 0, 69.0966))
print(f"(0 4 0) ? {sol.h:.2f} {sol.k:.2f} {sol.l:.2f}")

(0 4 0) ? 0.00 4.00 0.00

Check the forward calculation: (040)#

[16]:

sol = sixc.forward((0, 4, 0))
print(
    "(040) :",
    f"tth={sol.delta:.4f}",
    f"omega={sol.omega:.4f}",
    f"chi={sol.chi:.4f}",
    f"phi={sol.phi:.4f}",
    f"mu={sol.mu:.4f}",
    f"gamma={sol.gamma:.4f}",
    )

(040) : tth=69.0982 omega=-145.4502 chi=90.0000 phi=0.0000 mu=0.0000 gamma=0.0000

Scan in reciprocal space using Bluesky#

To scan with Bluesky, we need more setup.

[17]:

%matplotlib inline

from bluesky import RunEngine
from bluesky import SupplementalData
from bluesky.callbacks.best_effort import BestEffortCallback
from bluesky.magics import BlueskyMagics
import bluesky.plans as bp
import bluesky.plan_stubs as bps
import databroker
from IPython import get_ipython
import matplotlib.pyplot as plt

plt.ion()

bec = BestEffortCallback()
db = databroker.temp().v1
sd = SupplementalData()

get_ipython().register_magics(BlueskyMagics)

RE = RunEngine({})
RE.md = {}
RE.preprocessors.append(sd)
RE.subscribe(db.insert)
RE.subscribe(bec)

[17]:

(h00) scan near (400)#

In this example, we have no detector. Still, we add the diffractometer object in the detector list so that the hkl and motor positions will appear as columns in the table.

[18]:

RE(bp.scan([sixc], sixc.h, 3.9, 4.1, 5))



Transient Scan ID: 1     Time: 2023-11-20 21:55:45
Persistent Unique Scan ID: 'bfce2f8f-41dd-445f-9c27-7b7068df4382'
New stream: 'primary'
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|   seq_num |       time |     sixc_h |     sixc_k |     sixc_l |    sixc_mu | sixc_omega |   sixc_chi |   sixc_phi | sixc_gamma | sixc_delta |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|         1 | 21:55:45.9 |      3.900 |     -0.000 |     -0.000 |      0.000 |   -146.431 |     -0.000 |      0.000 |      0.000 |     67.137 |
|         2 | 21:55:47.1 |      3.950 |     -0.000 |     -0.000 |      0.000 |   -145.942 |      0.000 |      0.000 |      0.000 |     68.115 |
|         3 | 21:55:48.1 |      4.000 |     -0.000 |     -0.000 |      0.000 |   -145.450 |     -0.000 |      0.000 |      0.000 |     69.098 |
|         4 | 21:55:49.2 |      4.050 |     -0.000 |      0.000 |      0.000 |   -144.956 |     -0.000 |      0.000 |      0.000 |     70.087 |
|         5 | 21:55:50.3 |      4.100 |     -0.000 |     -0.000 |      0.000 |   -144.458 |     -0.000 |      0.000 |      0.000 |     71.083 |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
generator scan ['bfce2f8f'] (scan num: 1)

/home/prjemian/.conda/envs/bluesky_2023_3/lib/python3.11/site-packages/bluesky/callbacks/fitting.py:167: RuntimeWarning: invalid value encountered in scalar divide
  np.sum(input * grids[dir].astype(float), labels, index) / normalizer

[18]:

('bfce2f8f-41dd-445f-9c27-7b7068df4382',)

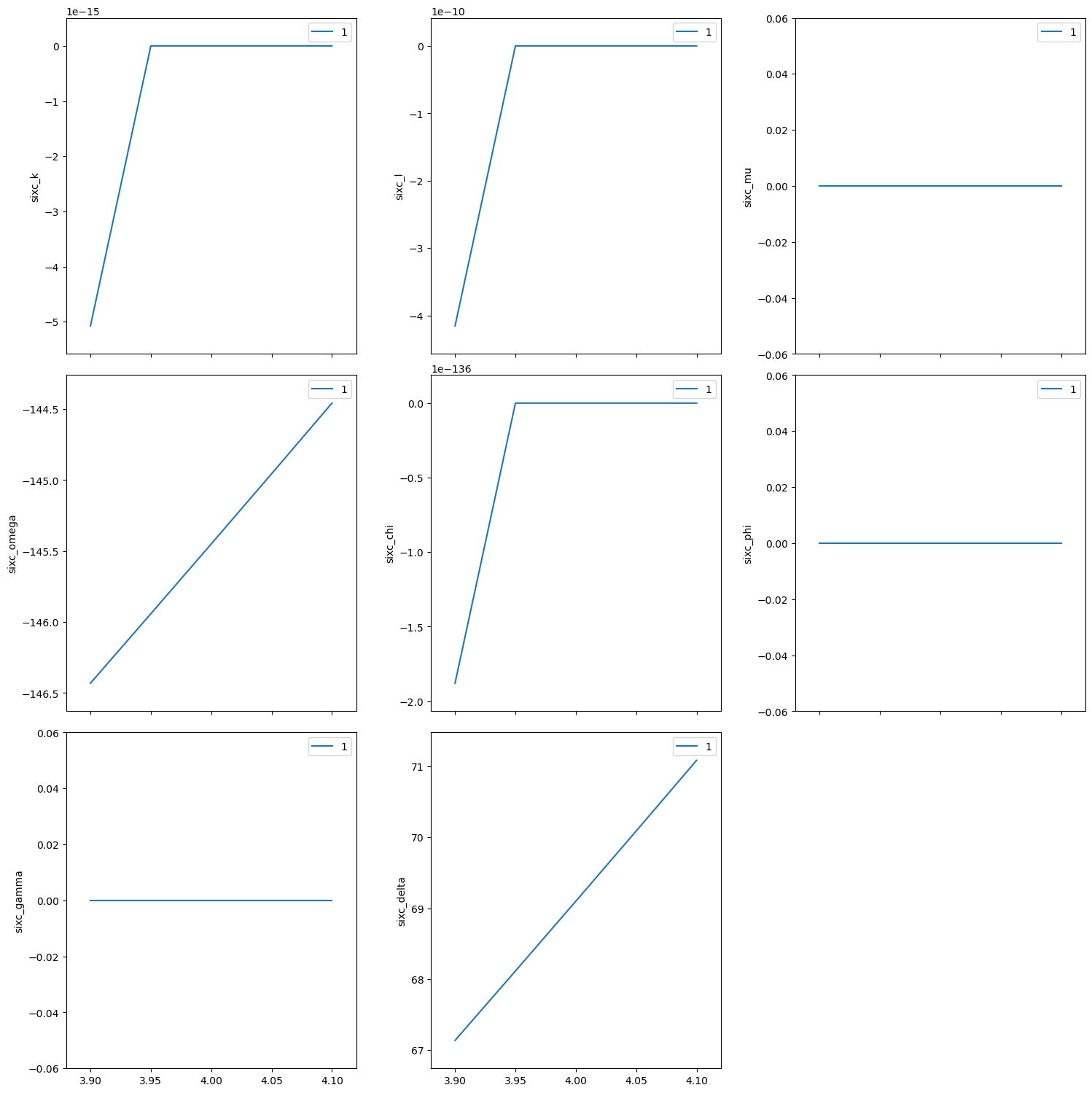
../../_images/examples_notebooks_geo_e6c_40_4.png

chi scan from (400) to (040)#

If we do this with $\omega=-145.451$ and $\delta=69.0966$, this will be a scan between the two orientation reflections.

Use %mov (IPython magic command) to move both motors at the same time.

[19]:

print("possible modes:", sixc.calc.engine.modes)
print("chosen mode:", sixc.calc.engine.mode)

# same as orientation reflections
%mov sixc.omega -145.4500 sixc.delta 69.0985

RE(bp.scan([sixc], sixc.chi, 0, 90, 10))

possible modes: ['bissector_vertical', 'constant_omega_vertical', 'constant_chi_vertical', 'constant_phi_vertical', 'lifting_detector_phi', 'lifting_detector_omega', 'lifting_detector_mu', 'double_diffraction_vertical', 'bissector_horizontal', 'double_diffraction_horizontal', 'psi_constant_vertical', 'psi_constant_horizontal', 'constant_mu_horizontal']
chosen mode: constant_phi_vertical


Transient Scan ID: 2     Time: 2023-11-20 21:55:53
Persistent Unique Scan ID: '2ba6e8a2-82c3-4259-b1f9-eb57ae800f93'
New stream: 'primary'
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|   seq_num |       time |   sixc_chi |     sixc_h |     sixc_k |     sixc_l |    sixc_mu | sixc_omega |   sixc_phi | sixc_gamma | sixc_delta |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|         1 | 21:55:53.4 |      0.000 |      4.000 |      0.000 |      0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         2 | 21:55:54.5 |     10.000 |      3.939 |      0.695 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         3 | 21:55:55.6 |     20.000 |      3.759 |      1.368 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         4 | 21:55:56.7 |     30.000 |      3.464 |      2.000 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         5 | 21:55:57.8 |     40.000 |      3.064 |      2.571 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         6 | 21:55:58.9 |     50.000 |      2.571 |      3.064 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         7 | 21:56:00.0 |     60.000 |      2.000 |      3.464 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         8 | 21:56:01.1 |     70.000 |      1.368 |      3.759 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|         9 | 21:56:02.2 |     80.000 |      0.695 |      3.939 |     -0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
|        10 | 21:56:03.3 |     90.000 |      0.000 |      4.000 |      0.000 |      0.000 |   -145.450 |      0.000 |      0.000 |     69.099 |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
generator scan ['2ba6e8a2'] (scan num: 2)

[19]:

('2ba6e8a2-82c3-4259-b1f9-eb57ae800f93',)

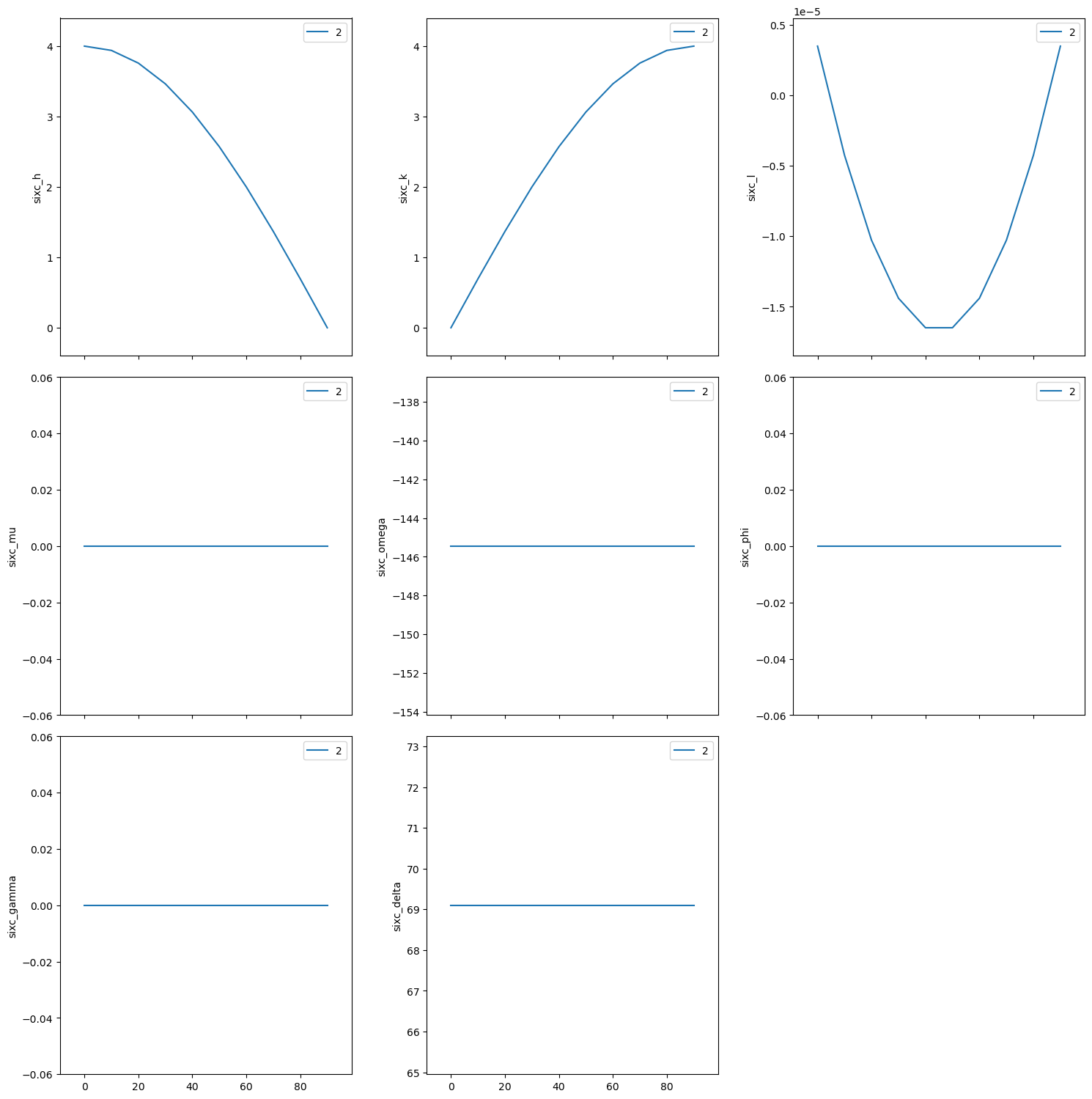
../../_images/examples_notebooks_geo_e6c_42_2.png

(0k0) scan near (040)#

[20]:

RE(bp.scan([sixc], sixc.k, 3.9, 4.1, 5))



Transient Scan ID: 3     Time: 2023-11-20 21:56:06
Persistent Unique Scan ID: 'ab43d500-fa03-4b67-ae53-a656a65e0eaf'
New stream: 'primary'
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|   seq_num |       time |     sixc_k |     sixc_h |     sixc_l |    sixc_mu | sixc_omega |   sixc_chi |   sixc_phi | sixc_gamma | sixc_delta |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|         1 | 21:56:06.2 |      3.900 |      4.100 |      0.000 |      0.000 |   -126.652 |     43.568 |      0.000 |      0.000 |    106.695 |
|         2 | 21:56:07.3 |      3.950 |      4.100 |     -0.000 |      0.000 |   -126.179 |     43.933 |      0.000 |      0.000 |    107.641 |
|         3 | 21:56:08.4 |      4.000 |      4.100 |     -0.000 |      0.000 |   -125.697 |     44.293 |      0.000 |      0.000 |    108.604 |
|         4 | 21:56:09.4 |      4.050 |      4.100 |     -0.000 |      0.000 |   -125.206 |     44.648 |      0.000 |      0.000 |    109.585 |
|         5 | 21:56:10.5 |      4.100 |      4.100 |     -0.000 |      0.000 |   -124.707 |     45.000 |      0.000 |      0.000 |    110.585 |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
generator scan ['ab43d500'] (scan num: 3)

[20]:

('ab43d500-fa03-4b67-ae53-a656a65e0eaf',)

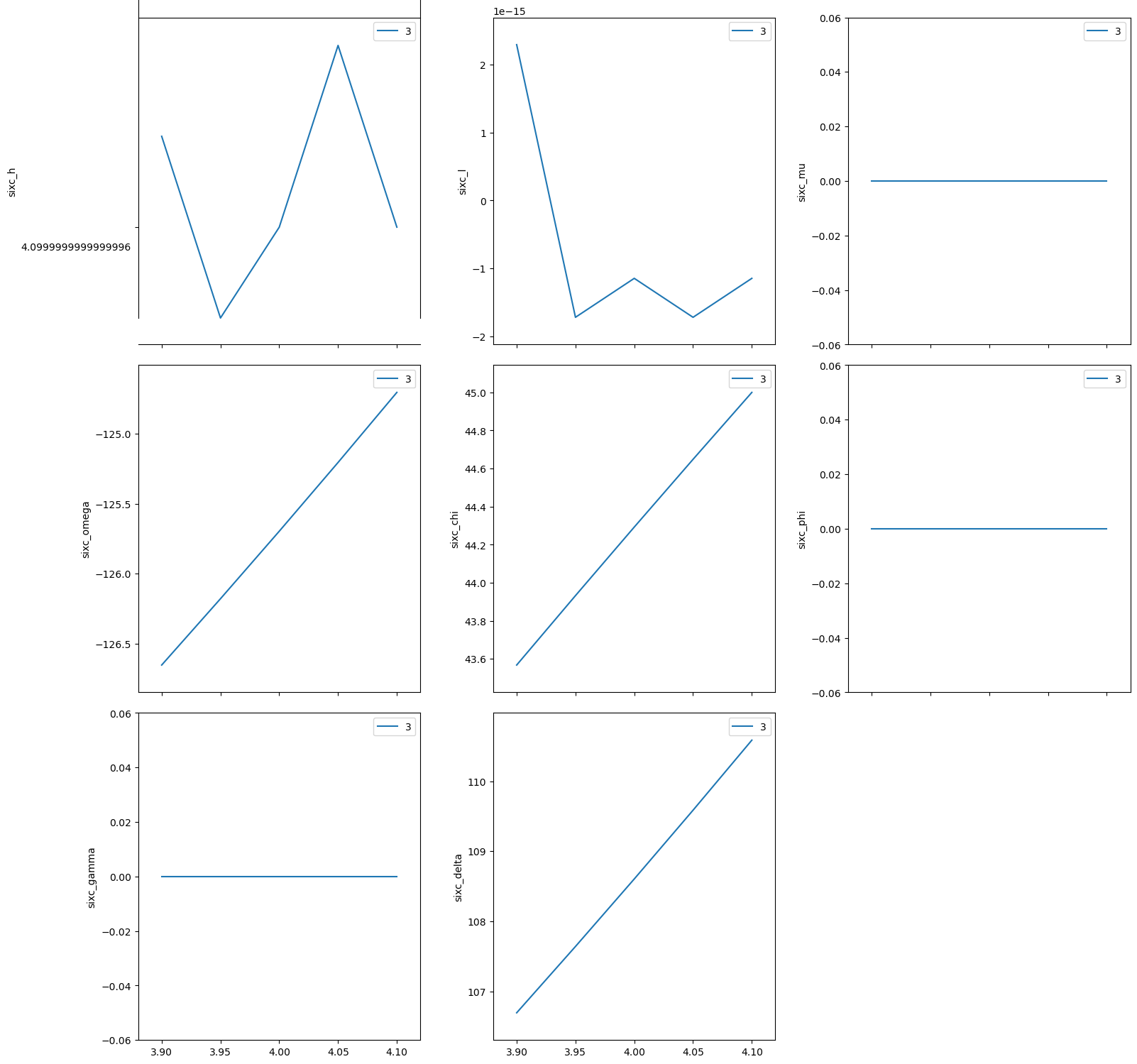
../../_images/examples_notebooks_geo_e6c_44_2.png

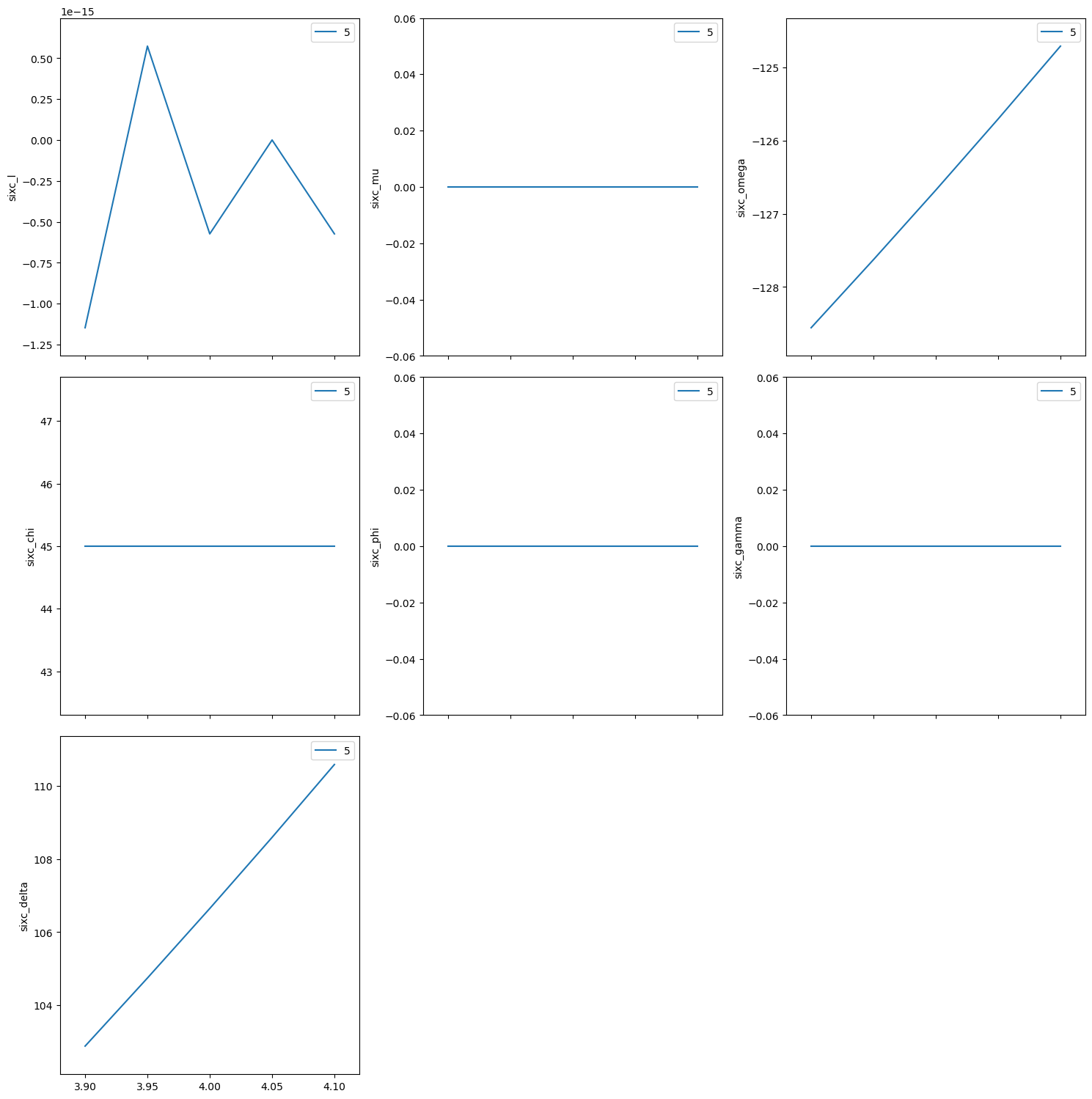
(hk0) scan near (440)#

[21]:

RE(bp.scan([sixc], sixc.h, 3.9, 4.1, sixc.k, 4.1, 3.9, 5))



Transient Scan ID: 4     Time: 2023-11-20 21:56:13
Persistent Unique Scan ID: 'e6252b02-1efb-4be3-8b4e-713be6486cba'
New stream: 'primary'
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|   seq_num |       time |     sixc_h |     sixc_k |     sixc_l |    sixc_mu | sixc_omega |   sixc_chi |   sixc_phi | sixc_gamma | sixc_delta |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|         1 | 21:56:13.4 |      3.900 |      4.100 |     -0.000 |      0.000 |   -126.652 |     46.432 |      0.000 |      0.000 |    106.695 |
|         2 | 21:56:14.2 |      3.950 |      4.050 |     -0.000 |      0.000 |   -126.670 |     45.716 |      0.000 |      0.000 |    106.659 |
|         3 | 21:56:15.1 |      4.000 |      4.000 |     -0.000 |      0.000 |   -126.676 |     45.000 |      0.000 |      0.000 |    106.647 |
|         4 | 21:56:15.9 |      4.050 |      3.950 |      0.000 |      0.000 |   -126.670 |     44.284 |      0.000 |      0.000 |    106.659 |
|         5 | 21:56:16.8 |      4.100 |      3.900 |      0.000 |      0.000 |   -126.652 |     43.568 |      0.000 |      0.000 |    106.695 |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
generator scan ['e6252b02'] (scan num: 4)

[21]:

('e6252b02-1efb-4be3-8b4e-713be6486cba',)

../../_images/examples_notebooks_geo_e6c_46_2.png

Move to the (440) reflection.

[22]:

sixc.move((4,4,0))
print(f"{sixc.position = }")

sixc.position = SixCirclePseudoPos(h=3.9999999999999973, k=3.9999999999999996, l=-1.1471889002931271e-15)

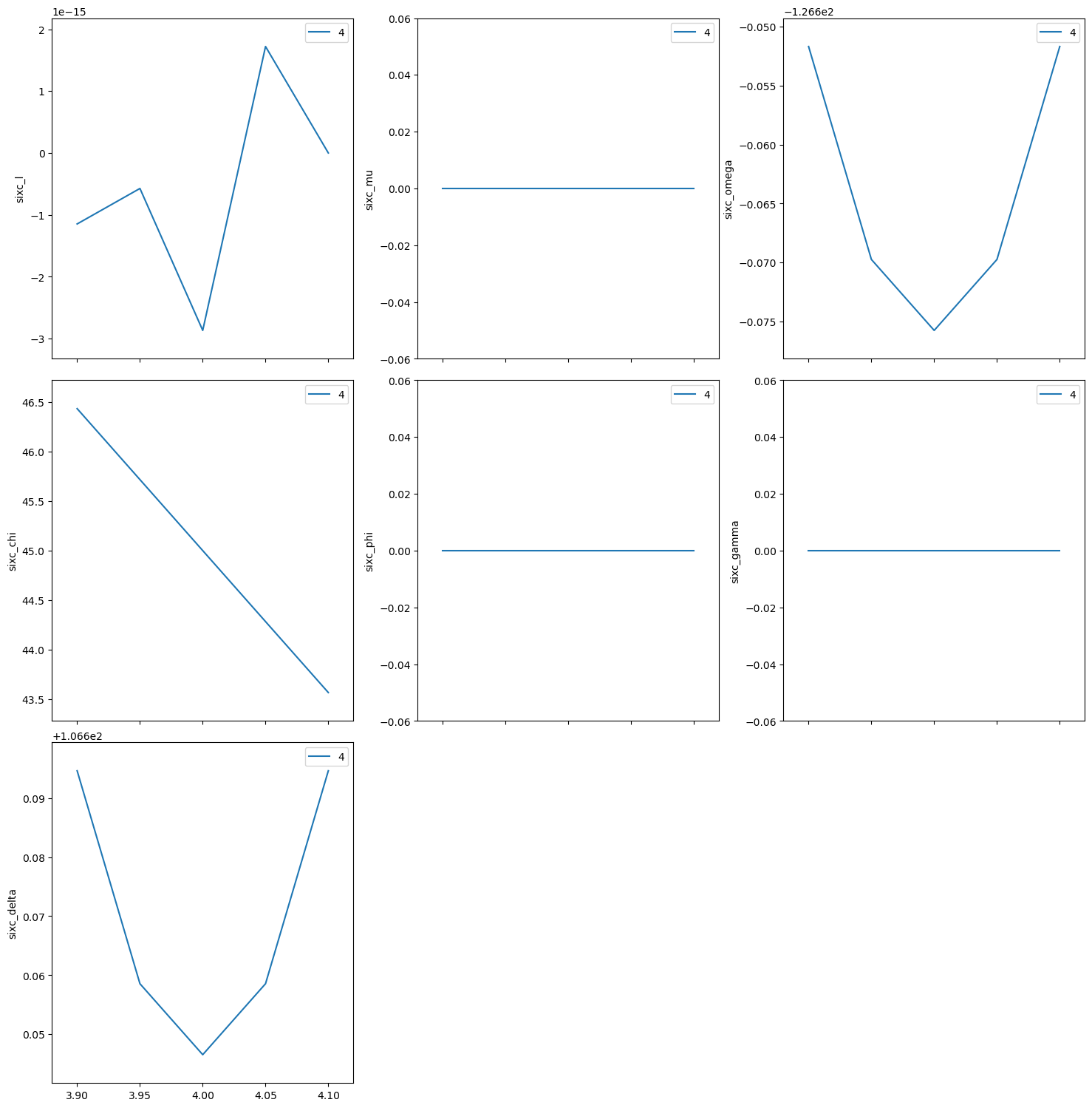
Repeat the same scan about the (440) but use relative positions.

[23]:

RE(bp.rel_scan([sixc], sixc.h, -0.1, 0.1, sixc.k, -0.1, 0.1, 5))



Transient Scan ID: 5     Time: 2023-11-20 21:56:19
Persistent Unique Scan ID: '60ac1e46-e2f3-4037-aadc-afdce36d1975'
New stream: 'primary'
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|   seq_num |       time |     sixc_h |     sixc_k |     sixc_l |    sixc_mu | sixc_omega |   sixc_chi |   sixc_phi | sixc_gamma | sixc_delta |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
|         1 | 21:56:19.3 |      3.900 |      3.900 |     -0.000 |      0.000 |   -128.558 |     45.000 |      0.000 |      0.000 |    102.882 |
|         2 | 21:56:20.3 |      3.950 |      3.950 |      0.000 |      0.000 |   -127.627 |     45.000 |      0.000 |      0.000 |    104.744 |
|         3 | 21:56:21.1 |      4.000 |      4.000 |     -0.000 |      0.000 |   -126.676 |     45.000 |      0.000 |      0.000 |    106.647 |
|         4 | 21:56:22.0 |      4.050 |      4.050 |      0.000 |      0.000 |   -125.703 |     45.000 |      0.000 |      0.000 |    108.592 |
|         5 | 21:56:22.9 |      4.100 |      4.100 |     -0.000 |      0.000 |   -124.707 |     45.000 |      0.000 |      0.000 |    110.585 |
+-----------+------------+------------+------------+------------+------------+------------+------------+------------+------------+------------+
generator rel_scan ['60ac1e46'] (scan num: 5)

[23]:

('60ac1e46-e2f3-4037-aadc-afdce36d1975',)

../../_images/examples_notebooks_geo_e6c_50_2.png

axis	moves	rotation axis	vector
mu	sample	\(\vec{z}\)	`[0 0 1]`
omega	sample	\(-\vec{y}\)	`[0 -1 0]`
chi	sample	\(\vec{x}\)	`[1 0 0]`
phi	sample	\(-\vec{y}\)	`[0 -1 0]`
gamma	detector	\(\vec{z}\)	`[0 0 1]`
delta	detector	\(-\vec{y}\)	`[0 -1 0]`